Let's talk about money! Shall we? Time value of money (TVM) is honestly my favorite topic to cover in Corporate Finance. If you have ever put money aside every month into a savings account for buying a house or a car, what makes it grow? This concept will help you understand how that happens. The students I've tutored before on this know that I get pumped up with excitement to have a privilege of teaching them Compound Interest - the eighth wonder of the world according Albert Einstein. I saw the need to compile 5 common mistakes students make when solving Time Value of Money (TVM) questions. This relates to calculating the following ;
Present Values (PV)
Future Values (FV)
Recurring payments (PMT)
Duration of investment (NPER)
Interest rate (I)
1. Not adjusting the rate(I), time(NPER) and recurring payment(PMT) in a multiple compounding problem.
In multiple compounding, interest is paid more than once a year. It could be semiannually, quarterly, monthly or daily or continuously. Forgetting to convert the interest rate (I) , duration of investment (NPER) and recurring payment (PMT) as per the number of compounding periods per year is a common mistake I've observed students make. This applies for calculation of PV or FV of a one-time cashflows and annuities. I'll give an example below;
Jane deposited $500 in a savings account that earns 10% compounded semiannually. What will be the value of her savings in 2 years?
Using 10% as the semiannual rate is incorrect. Here's the right way to solve it ;
Solution:
It is important to identify that interest is paid semiannually; meaning every six months or twice per year.
Next, convert the annual rate to semiannual rate by dividing 10% by the number of compounding periods per year(2) to get 5% .
The duration of investment is 2 years and there will be 2 interest payments per year; meaning in 2 years, Jane's account will have a total of 4 interest payments(2*2 =4)
Future value will be ; FV = 500 (1.05)^4
FV = 500*1.215506
FV= $607.75
2. Using Effecting Annual Rate(EAR) to calculate for nominal amount without converting it to Annual Percentage Rate (APR).
This is another trap that can make a student lose points. EAR is the rate that you actually earn on your savings or investments while APR is the quoted rate or nominal rate you see at then bank or a lending institution. For example, if a questions says " Brian plans to house in 5 years and he can afford to save $2,000 per month . If he earns an EAR of 10 percent before , how much will he have accumulated at the end of 5 years? "
Using the the 10% EAR to calculate the nominal future amount without converting to APR is incorrect. To get the right answer, use the following APR-EAR conversion formulas.
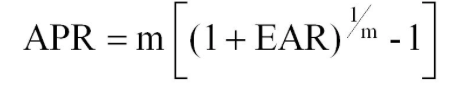
Since we are looking for APR , use the first formula to get the nominal rate as follows;
The correct rate to use will be 9.57% .
3. Assuming One-time cashflow means the same thing as Annuities.
In a one time cash-flow, someone deposits money into an account only once and does not add any other deposits. That principal amount earns interest which when reinvested, earn another interest through a process called compounding. Annuities on the other hand, are equally recurring cashflows. The example I used above above example I used; "Jane deposited $500 in a savings account that earns 10% compounded semiannually. What will be the value of her savings in 2 years? " is a one-time cashflow; Jane deposited the $500 once and let it grow. On the other hand , if the question was framed this way;
" Jane deposited $500 in a savings account at the end of every 6 months for 5 years..." then this would be considered a recurring cashflow or an Annuity.
4. Confusing Annuity Due and Ordinary Annuity
If you find annuities to be complicated , you are not alone. Apparently, 70% of the students I tutored it to found it challenging. However, fortunately enough, they were able to get it right once they understood one simple but important factor which is; at what point does the recurring cashflow occur. This brings us to the difference between an Ordinary annuity and Annuity Due.
In Ordinary annuity, the recurring equal cashflows occur at the end of each period. i.e end of every year, end of every month, end of every week or end of every day .
Annuity Due is the opposite; the recurring equal cashflows occur at the beginning of each period. i.e beginning of every year, beginning of every month, beginning of every week or beginning of every day .
5.Using Incorrect formulas
Wrong formulas can be detrimental to your overall score either in an assignment or even in a main exam. If you have taken a couple Finance courses for a while , I bet by now you have noticed that there is quite a number of Finance formulas applicable in different scenarios and to be honest, memorizing them can be an uphill task. A tip that works for me is making sure I read carefully and understand the questions, then relate it to a Finance concept.
Examples;
a.) What is the present value of $10,000 to be received in 10 years at 8% compounded annually?
Concept : present value
Formula : PV = FV/(1+r)^n
b.) What is the future value of $2,000 invested at the end of each year for 25 years at 5% compounded annually?
Concept: Ordinary annuity
Formula:
c.) What is the future value of $3,000 invested for 10 years at 5% compounded annually
Concept: Future value
Formula: FV = PV(1+r)^n
Comments